✨Định Lý Cuối Cùng Của Fermat
Định Lý Cuối Cùng Của Fermat
Siêu Nhí Khám Phá: Toán Tư Duy - Phát Triển Toàn Diện IQ Toán Học Dành Cho Bé Từ 3 - 4 Tuổi Tác giả 1980Edu NXB NXB Dân Trí Năm XB 2022 Ngôn Ngữ
Phiếu Bài Tập Cuối Tuấn Môn Toán Lớp 3 (Biên Soạn Theo Chương Trình GDPT Mới) Được biên soạn bám sát chương trình Giáo dục Tiểu học, theo Chương trình mới của Bộ Giáo dục
Công ty phát hànht1980 Books Tác giảtHiroyuki Irie Người DịchtLại Minh Tâm NXBtNXB Công Thương Năm XBt2020 Ngôn NgữtTiếng Việt Trọng lượng (gr)t350 Kích Thước Bao Bìt20 x 13 cm Số trangt344 Hình thứctBìa Mềm
Combo Sách Học Tiếng Nhật Hay( Bản Tiếng Nhật): Tiếng Nhật Cho Mọi Người - Trình Độ Sơ Cấp 1 - Bản Tiếng Nhật - (Tái Bản) + Tiếng Nhật Cho Mọi Người - Sơ
Bách Khoa Tri Thức Phổ Thông - 10 Vạn Câu Hỏi Vì Sao? Bách Khoa Tri Thức Phổ Thông - 10 Vạn Câu Hỏi Vì Sao? là cuốn sách thuộc tủ sách kiến thức phổ
Combo Sói già Phố Wall trọn bộ 2 tập tái bản (tặng kèm bookmark thiết kế aha) Bộ truyện lên tiếng về sự tham lam, lối sống xa hoa vô độ của 1 số bộ
Nếu bố mẹ đang tìm kiếm những cuốn sách không đặt nặng vấn đề kiến thức nhưng lại khơi gợi được hứng thú học tập cho trẻ, giúp các con tự tin hơn, tiếp thu
Với cuốn sách luyện thi đại học môn hóa học Phân Loại Và Phương Pháp Giải Nhanh Bài Tập Hóa Hữu Cơ của tác giả Quan Hán Thành, gồm có 6 phần. Phần 1 :
Combo Đề Kiểm Tra Toán Lớp 6 - Tập 1+2 (Biên Soạn Theo Chương Trình Giáo Dục Phổ Thông Mới) 1. Đề Kiểm Tra Toán Lớp 6 - Tập 1 Quý thầy cô cùng các
Học Tiếng Anh Bằng Hình Ảnh Lớp 1 sẽ cung cấp cho các em học sinh những từ vựng quan trọng. Khi nhìn thấy hình ảnh tương ứng với một từ, bạn sẽ nhớ được
Combo The Small Big – Tuyệt Chiêu Thuyết Phục, Hạ Gục Khách Hàng + 7 Loại Hình Thông Minh (Bộ 2 Cuốn) Thành công thuyết phục người khác thực hiện hành động cụ thể là
Một thế giới không có đàn bà là tiểu thuyết của nhà văn Bùi Anh Tấn, được chuyển thể thành phim cùng tên nằm trong Series Cảnh sát hình sự đình đám một thời. Truyện
Combo Trọn Bộ 5 Cuốn Chiến Tranh Tiền Tệ ( Tập 1+2+3+4+5 ) Song Hong Bing Tập 1 – Ai thật sự giàu nhất thế giới? Tập 2 – Sự Thống Trị Của Quyền Lực
“Evie và chuyến phiêu lưu ở rừng nhiệt đới” Là phần tiếp theo của cuốn “Evie và biệt tài bí mật” của tác giả Matt Haig, tác giả có sách bán chạy nhất ở Anh.
Tập Viết Lớp 1 Tập Viết Lớp 1 giúp các em học sinh lớp 1 tập viết, rèn chữ, bước đầu làm quen với các con chữ, chữ số. Với các nét mẫu để các
Nghệ Thuật Quản Lý Tài Chính Cá Nhân TIỀN BẠC là niềm đam mê bất tận và nỗi khổ đau cùng cực của nhân loại, là chủ đề cực độ nhạy cảm nhưng tột cùng
Tại Sao Các Quốc Gia Thất Bại (Tái bản năm 2024) (Nobel Kinh tế 2024) Nhà xuất bản : NXB Trẻ. Công ty phát hành : NXB Trẻ. Tác giả : Daron Acemoglu. Kích thước
Bộ gồm 3 quyển: 1. Ehon Nhật Bản - Bé Trai Đi Toilet - Cuốn sách đáng yêu này rèn bé trai 1-5 tuổi cách tự đi vệ sinh sạch sẽ và an toàn -
FOREX 100% – HỌC CÁCH KIẾM TIỀN TRÊN THỊ TRƯỜNG Forex là thị trường ngoại hối quốc tế. Giá trị giao dịch trung bình hàng ngày của nó ước đạt 3 nghìn tỷ đô-la Mỹ.
Chinh Phục Đề Thi 9 Vào 10 Chuyên Hóa Học Đối với mỗi học sinh yêu thích và có năng khiếu về bộ môn Hóa học thì đều có ước mơ được học vào các
Jim Collins là tác giả của hai đầu sách nổi tiếng - Từ tốt đến vĩ đại và Xây dựng để trường tồn. Cùng với phương pháp nghiên cứu như hai cuốn đầu tiên, trong
Combo Truyện Trinh Thám hấp dẫn: Nguồn Cội - Origin + Biểu Tượng Thất Truyền / Sách Hay Của Dan Brown Top 100 truyện trinh thám bán chạy nhất trong tháng! Hàng triệu độc giả
Thông tin chi tiết: 1. Thơ gia đình yêu thương : Thơ về ông Công ty phát hành: Đại Mai Tác Giả: Mai Hương Số trang: 25 Năm xuất bản : 2023 Khổ sách:19x22cm Hình
Sách Cảnh Sắc Đà Lạt - Xứ Ngàn Hoa: Tranh Và Ký Họa ------------ Cảnh Sắc Đà Lạt - Xứ Ngàn Hoa: Tranh Và Ký Họa Nhà xuất bản : Nhà Xuất Bản Thế Giới.
Hiện nay đã có một số sách dạy tiếng Việt cho người nước ngoài. Mỗi cuốn sách có mục tiêu, yêu cầu của mình trong việc biên soạn. Bộ Tiếng Việt cho người nước ngoài
AI NÊN ĐỌC CUỐN SÁCH NÀY? Sau nhiều năm lao động vất vả, bạn đã dành dụm được số tiền lớn để thực hiện ước mơ “an cư lạc nghiệp”. Ngôi nhà là một tài
Combo Big 4 Bộ Đề Tự Kiểm Tra 4 Kỹ Năng Nghe - Nói - Đọc - Viết (Cơ Bản Và Nâng Cao) Tiếng Anh Lớp 9 (2 Tập) viết theo chuẩn khung chương trình
Hiền Ngu Nhân Duyên Kinh có bốn mươi sáu (46) câu truyện do chính đức Phật kể lại về tiền thân của ngài, thỉnh thoảng vẫn có những đoạn nói về hàng môn nhân đệ
Understanding Digital Marketing - Thông Thạo Digital Marketing Nhà xuất bản : Nhà Xuất Bản Hồng Đức. Công ty phát hành : Văn Lang. Tác giả : Damian Ryan. Kích thước : 24 x 16
OSHO - Trò Chuyện Với Vĩ Nhân ------------ Trò chuyện với vĩ nhân “Trò chuyện với vĩ nhân” tổng hợp những câu chuyện của thiền sư Osho về 20 triết gia, nhà tư tưởng, đạo
Bộ sách Kỹ năng sinh tồn dành cho trẻ trọn bộ 4 cuốn đề cập đến tất cả những mối nguy hiểm tiềm ẩn có thể ảnh hưởng đến sự an toàn của trẻ nhỏ
Combo OCEAN – Thuyết Minh Trực Quan Nhất Về Đại Dương và Những Câu Hỏi Lớn - Vũ Trụ OCEAN – Thuyết Minh Trực Quan Nhất Về Đại Dương CUỘC SỐNG CŨNG NHƯ BIỂN CẢ,
COMBO 2 CUỐN SÁCH: QUẢN TRỊ MỤC TIÊU BẰNG KPI, BSC & OKR, SÁCH 100 + 25 CÂU HỎI BSC & KPI VÀ SÁCH HIỆN TƯỢNG RĐ - SỐNG SÓT TRONG DÒNG XOÁY CHUYỂN ĐỔI
Cách Những Công Ty Lớn Nhất Thế Giới Sinh Tồn Nhà xuất bản : NXB Trẻ. Công ty phát hành : NXB Trẻ. Tác giả : Liz Hoffman. Kích thước : 20.5 x 13 x
Qua những câu chuyện cổ về ngày xửa ngày xưa phảng phất sắc màu huyền diệu, đất nước Kazakhstan hiện lên như một bức tranh tươi đẹp, khoáng đạt và huyền bí. Theo những bước
Cuốn sách được biên tập gồm 2 phần: Hóa học Hữu cơ và Hóa học Vô cơ. Ở mỗi phần, tác giả đều trình bày 2 phần chính: Phần thứ nhất là những kiến thức
Combo Phiếu Bài Tập Cuối Tuấn Môn Toán + Tiếng Việt + Tiếng Anh Lớp 3 (Biên Soạn Theo Chương Trình GDPT Mới) (Bộ 3 Cuốn) Bộ sách tham khảo lớp 3 này gồm có:
Combo 2 cuốn sách khởi nghiệp hay: Bước Đi Ngẫu Nhiên Trên Phố Wall + Phương pháp đầu tư Warren Buffett (tặng kèm bookmark thiết kế aha) 1,Bước Đi Ngâu Nhiên Trên Phố Wall Dù
Chắc hẳn khi mới đọc tiêu đề thôi thì 100% người chưa biết chữ Hoa hay mới học chữ Hán sẽ “rất sợ”. Thậm chí ngay cả đối với những người đã học xong Hoa
10 Thói Quen Của Triệu Phú Tự Thân Trong thế giới hiện đại ngày nay, chúng ta đang đi nhanh hơn bao giờ hết, thế nhưng ta chỉ đang đi rất nhanh trên chiếc máy
Vùng Đất Nam Bộ Dưới Triều Minh Mạng ( 1820 - 1841) Mục đích của cuốn sách này nhằm làm sáng tỏ một loạt những sự kiện chính trị quan trọng đã diễn ra ở
Trò Chơi Màu Sắc Dành Cho Gấu Mèo Chester Và Kẻ Bắt Nạt To Xác Xấu Xa – A Color Game For Chester Raccon Cuốn sách nằm trong sê-ri Nụ hôn trên bàn tay –
Còn sống và bước đi trên mặt đất này là một phép lạ, nhưng hầu hết chúng ta lại chạy đi tìm hạnh phúc ở một nơi xa xôi nào đó như thể là có
Sách Ehon - Chơi Thể Thao Cùng Kenta (Combo 6 cuốn) ----------------------------------------- Lời nói dầu/ Giới thiệu sách - Cũng như đa phần những đứa trẻ ở độ tuổi từ 6-8, Kenta khao khát được
Giáo Trình Marugoto - Sơ Cấp 2 - A2 - Hiểu Biết Ngôn Ngữ Văn Hóa Nhật Ngay sau khi ra mắt bộ giáo trình Marugoto A2 Sơ cấp 1, First News – Trí Việt
Toán Học Cho Trẻ Mẫu Giáo: Lớp Lá 2 Bộ sách Toán học cho trẻ mẫu giáo mỗi cuốn có lý thuyết (đơn giản) và các bài tập thực hành về số đếm, hình dạng,
Phật nói ra một vạn một ngàn một trăm vị Phật, tuy có vị trùng danh, nhưng chẳng phải trùng Phật, chúng ta đọc hết bộ kinh này, như đến được cảnh giới Phật, thật
" CHÚNG TÔI DÀNH 10% LỢI NHUẬN TỪ BÁN SÁCH ỦNG HỘ QUỸ TRẺ EM ĐẾN TRƯỜNG" Biết ơn quý độc giả góp phần giúp đỡ trẻ em có hoàn cảnh khó khăn có cơ
100 Truyện Cổ Tích Thế Giới (Bìa Cứng) (Tái Bản 2019) Công ty phát hành Nhà sách Minh Thắng Tác giả Trần Trường Minh Ngày xuất bản 01-2019 Kích thước 13.5 x 20.5 cm Phiên
Công ty phát hành: Nhân Trí Việt Tác giả: Andrew Betsis, Lawrence Mamas Năm Xuất Bản: 08-2014 Kích thước: 21 x 29.7 cm Nhà Xuất Bản Tổng hợp Loại bìa: Bìa mềm Số trang: 223
Trong những trang sách giàu tưởng tượng và tươi vui dí dỏm này, tác giả đã xây dựng nên một thế giói các cô các chú tí hon hết sức tinh nghịch và ngộ nghĩnh.
Bộ não tí hon Tập 1: Cái nôi của thiên tài Cách những bậc cha mẹ thông minh nuôi dạy những đứa trẻ thông minh Phần lớn các bộ phận cơ thể người, sự phát
Tổng Quan Về Tarot (Bìa Cứng) ------------ TỔNG QUAN VỀ TAROT Từ điển từ khóa và diễn giải ý nghĩa của từng lá bài Tarot và đời sống Về bản chất, Tarot chính là những
Hẳn các bậc phụ huynh từng có những lúc nghĩ rằng: “Con mình còn nhỏ nên không thể ép uổng vô lí” hoặc “Bố mẹ dọn thì nhanh hơn” và âm thầm dọn dẹp hộ
Việc học tập phân môn Văn học trong Ngữ văn của các em, phần lớn Y trong nhà trường phổ thông thường nhìn ở kết quả một bài viết theo một đề bài nhất định. Đây
Trật Tự Thế Giới (Tái Bản 2018) Trong tác phẩm, Kissinger xuất phát từ Hòa ước Westphalia để phân tích về tương quan giữa các nước, chủ yếu là các cường quốc và các khu
Căng thẳng vẫn leo thang trong khu rừng nơi bốn tộc mèo cư ngụ. Khi lòng trung thành dần chuyển dịch, mèo trước kia là bạn có thể trở thành thù chỉ sau một đêm,
Đến với cuốn sách Sông ngòi xông xênh bạn đọc sẽ không hề cảm thấy những rắc rối khi học môn địa lý mà chỉ toàn những chuyện rùng mình như: Hét lên lanh lánh!
Search Inside Yourself - Tạo Ra Lợi Nhuận Vượt Qua Đại Dương Và Thay Đổi Thế Giới Tất cả chúng ta đều biết công cụ tìm kiếm Google và công ty Google với văn hóa
Với Happy for No Reason - Khi mọi điểm tựa đều mất, tác giả Marci Shimoff đã có một cuộc cách mạng về quan niệm hạnh phúc. Trong khi phần lớn những quyển sách ở
👁️ 1 | ⌚2025-09-12 23:41:21.153
VNĐ: 126,000
Mua hàng tại Shopee giảm thêm 30%



VNĐ: 126,000
Mua hàng tại Shopee giảm thêm 30%



Định Lý Cuối Cùng Của Fermat - Một Mật Mã Huyền Bí Và Định Mệnh Trong lịch sử phát triển của toán học có lẽ không có định lý nào nổi tiếng như Định lý
Trong lịch sử phát triển của toán học có lẽ không có định lý nào nổi tiếng như Định lý cuối cùng của Fermat. Nó nổi tiếng vì dạng của nó quá đơn giản.
Khoa Học Khám Phá - Định Lý Cuối Cùng Của Fermat “xn + yn = zn, trong đó n = 3, 4, 5… vô nghiệm Tôi đã có một chứng minh thực sự tuyệt
Khoa Học Khám Phá - Định Lý Cuối Cùng Của Fermat - Hành Trình Đi Tìm Lời Giải Cho Bài Toán Khó Bậc Nhất Trong Lịch Sử “xn + yn = zn, trong đó n
Định Lý Cuối Cùng Của Fermat
“xn + yn = zn, trong đó n = 3, 4, 5… vô nghiệm Tôi đã có một chứng minh thực sự tuyệt vời cho mệnh đề này, nhưng do lề quá hẹp không thể
“xn + yn = zn, trong đó n = 3, 4, 5… vô nghiệm Tôi đã có một chứng minh thực sự tuyệt vời cho mệnh đề này, nhưng do lề quá hẹp không thể
Giới thiệu tóm tắt tác phẩm: “xn + yn = zn, trong đó n = 3, 4, 5… vô nghiệm Tôi đã có một chứng minh thực sự tuyệt vời cho mệnh đề này, nhưng
Được xem là quyển sách viết về toán học dành cho đại chúng đầu tiên trở thành best - seller " Tôi đã có một chứng minh thực sự tuyệt vời cho mệnh đề này,
Combo Sách Kiến Thức Bách Khoa Hay : Những Câu Hỏi Lớn Vật Lý + Những Câu Hỏi Lớn Toán Học ( Tặng Kèm Postcard HAPPY LIFE ) Hai cuốn sách Những Câu Hỏi Lớn
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
Những Câu Hỏi Lớn đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
Bộ 2 cuốn sách tìm hiểu về lịch sử toán học: Toán Học Một Thiên Tiểu Thuyết - Những Câu Hỏi Lớn Toán Học - Toán Học Một Thiên Tiểu Thuyết Hầu hết mọi người
Những Câu Hỏi Lớn - Toán Học NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
Lý thuyết số sơ cấp - Phương pháp sơ cấp trong lý thuyết số - Bản ĐB (Bìa cứng - Chữ kí của tác giả: GS.Ngô Bảo Châu) - Tác giả: GS. Ngô Bảo
Lý thuyết số sơ cấp - Phương pháp sơ cấp trong lý thuyết số - Tác giả: GS. Ngô Bảo Châu - TS. Đỗ Việt Cường - Nhà xuất bản Đại học Quốc gia Hà
Lý thuyết số, từ nhiều góc độ, được xem là điểm khởi đầu của toán học. Không chỉ là nơi khơi nguồn cho nhiều nhánh toán học phát triển, mà nó còn đem đến những
Tác giả: Sigmund Freud Người dịch: Phan Quang Định Ngôn ngữ: Tiếng Việt Năm xuất bản: 2024 Số trang: 182 Nhà phát hành: Thời Đại Nhà xuất bản: Tri Thức Kích thước: 13.5 x 20.5
Chư Kinh Nhật Tụng - Bìa Cứng Kinh có nghĩa là lời của Phật, Bồ Tát hay chư Tổ dạy cho đệ tử được ghi chép lại, những lời này là Chân Lý không thể
Something strange is happening in the Black Mountains: people are disappearing, government equipment is being stolen and destroyed, and the miners are in revolt. Countries occupied for centuries by the Black Empire are declaring their
Tác giả: 1980Edu (Phí Mai) Người dịch: THÔNG TIN XUẤT BẢN: Kích thước khổ: 20 x 20 Số trang: 24 Mã EAN: 8936066695923 NXB liên kết: NXB Dân Trí Sách do Công ty TNHH Văn
Tác giả: Lục Vũ Dịch giả: Trần Quang Đức Nhà xuất bản: Hội nhà văn Số trang: 188 Kích thước: 14x20.5 cm Ngày phát hành: 04-2022 Lục Vũ, người được suy tôn là ông thánh
Tác giả: TÔ MINH NGUYỆT Sinh 1944, quê làng Láng, Hà Nội. Tốt nghiệp Đại học Tổng hợp (Khoa Ngữ văn). Cán bộ kỹ thuật Nhà máy ô tô Hòa Bình. Phóng viên báo Phụ
Thảm lót sàn xe ô tô BMW 1 series 2020- nhãn hiệu Macsim 3W - chất liệu nhựa TPE được công ty TNHH Aladdin Asia đặt hàng từ nhà máy sản xuất uy tín hiện
NGOẠI NGỮ KHÓ ĐẤY NHƯNG BẠN TỰ HỌC ĐƯỢC - Bí quyết tự học chinh phục song ngữ Anh, Trung - Việt Lê - (bìa mềm) - Giá bìa: 168.000đ Học ngoại ngữ rất quan
Tự Chữa Lành - Làm Sao Để Khai Sáng - Tập 2 Bạn sẽ không thể phát triển được nếu như không bị phá vỡ để ánh sáng có thể chiếu vào cho phép
- Miễn phí VC nội thành - Giao hàng miễn phí tận nơi, thanh toán khi đã kiểm tra và nhận hàng - Được đổi trả trong vòng 24h với chính sách đặc biệt thuận
Đôi nét về tác phẩm: “Điều làm tôi ngạc nhiên nhất về nhân loại là chính bản thân con người. Họ hy sinh sức khỏe để kiếm tiền. Sau đó họ hy sinh tiền bạc
Mã hàng 8935280912014 Tên Nhà Cung Cấp Thái Hà Tác giả Mitsuko Tateishi Dịch giả Dạ Hương NXB NXB Lao Động Năm XB 2022 Trọng lượng (gr) 240 Kích Thước Bao Bì 19 x 13
ジョジョリオン 22 (ジャンプコミックス) - JOJORION 22
Tại sao tôi muốn viết cuốn sách này? 40 năm với tôi là một hành trình dài để chữa lành và trưởng thành, để “chọn bạn mà chơi”, để nhìn lại những năm tháng học
NỘI DUNG SÁCH Để đáp ứng yêu cầu đổi mới cách đánh giá học sinh trong môn Ngữ văn cấp THCS – CT 2018 (tránh dùng lại các văn bản đã học trong sách giáo
Những Nhà Tư Tưởng Lớn - Hegel Trong 60 Phút HEGEL là triết gia đầu tiên đã nhìn ra chiều kích của sự "trở thành" trong toàn bộ tầm mức của nó. Lịch sử nhân
sinh giỏi toán THCS, thi tuyển sinh lớp 10 trường chuyên và năng khiếu. Trong quá trình học toán và dạy toán , chúng tôi đã tổng hợp và phân loại các phương pháp giải
. ĐÂY LÀ RẬP BẰNG GIẤY, KHÔNG PHẢI QUẦN ÁO MẶC ĐƯỢC, Rập được in từ giấy A0 – Dạng bảng vẽ, không phải sản phẩm. Rập đã được may thử, hợp với vải thô,
Nghe Nói Tôi Rất Nghèo - Tập 3 Nhà xuất bản : Nhà Xuất Bản Dân Trí. Công ty phát hành : HNovels. Tác giả : Tô Cảnh Nhàn. Kích thước : 15.7 x 24
**Chứng minh của Wiles về định lý cuối cùng của Fermat** là chứng minh toán học của nhà toán học người Anh Andrew Wiles về một trường hợp đặc biệt của định lý Module đối
Định Lý Cuối Cùng Của Fermat - Một Mật Mã Huyền Bí Và Định Mệnh Trong lịch sử phát triển của toán học có lẽ không có định lý nào nổi tiếng như Định lý
Định Lý Cuối Cùng Của Fermat - Một Mật Mã Huyền Bí Và Định Mệnh Trong lịch sử phát triển của toán học có lẽ không có định lý nào nổi tiếng như Định lý
Trong lịch sử phát triển của toán học có lẽ không có định lý nào nổi tiếng như Định lý cuối cùng của Fermat. Nó nổi tiếng vì dạng của nó quá đơn giản.
Khoa Học Khám Phá - Định Lý Cuối Cùng Của Fermat “xn + yn = zn, trong đó n = 3, 4, 5… vô nghiệm Tôi đã có một chứng minh thực sự tuyệt
Khoa Học Khám Phá - Định Lý Cuối Cùng Của Fermat - Hành Trình Đi Tìm Lời Giải Cho Bài Toán Khó Bậc Nhất Trong Lịch Sử “xn + yn = zn, trong đó n
Định Lý Cuối Cùng Của Fermat
phải|Bài toán II.8 trong _Arithmetica_ của Diophantus, với chú giải của Fermat và sau đó trở thành định lý Fermat cuối cùng (ấn bản 1670) **Định lý cuối cùng của Fermat** (hay còn gọi là
“xn + yn = zn, trong đó n = 3, 4, 5… vô nghiệm Tôi đã có một chứng minh thực sự tuyệt vời cho mệnh đề này, nhưng do lề quá hẹp không thể
phải|nhỏ|389x389px|[[Định lý Pythagoras|Định lý Pitago có ít nhất 370 cách chứng minh đã biết ]] Trong toán học và logic, một **định lý** là một mệnh đề phi hiển nhiên đã được chứng minh là
“xn + yn = zn, trong đó n = 3, 4, 5… vô nghiệm Tôi đã có một chứng minh thực sự tuyệt vời cho mệnh đề này, nhưng do lề quá hẹp không thể
Giới thiệu tóm tắt tác phẩm: “xn + yn = zn, trong đó n = 3, 4, 5… vô nghiệm Tôi đã có một chứng minh thực sự tuyệt vời cho mệnh đề này, nhưng
Được xem là quyển sách viết về toán học dành cho đại chúng đầu tiên trở thành best - seller " Tôi đã có một chứng minh thực sự tuyệt vời cho mệnh đề này,
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
Những Câu Hỏi Lớn - Toán Học NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại
**Định lý của Ribet** (hay **Phỏng đoán Epsilon - Phỏng đoán ε**, tiếng Anh: **Ribet's theorem**) là một phần của lý thuyết số. Nó đề cập tới đến các thuộc tính của các biểu diễn
**Pierre de Fermat** (, phiên âm: _"Pi-e Đờ Phéc-ma"_, 17 tháng 8 năm 1607 ## Công việc Công trình tiên phong của Fermat trong Hình học giải tích (_Methodus ad disquirendam maximam et minimam et
**Lý thuyết số đại số** là một nhánh của lý thuyết số sử dụng các kỹ thuật của đại số trừu tượng để nghiên cứu các số nguyên, các số hữu tỷ và các tổng
Combo Sách Kiến Thức Bách Khoa Hay : Những Câu Hỏi Lớn Vật Lý + Những Câu Hỏi Lớn Toán Học ( Tặng Kèm Postcard HAPPY LIFE ) Hai cuốn sách Những Câu Hỏi Lớn
nhỏ|Các bảng số học dành cho trẻ em, Lausanne, 1835 **Số học** là phân nhánh toán học lâu đời nhất và sơ cấp nhất, được hầu hết mọi người thường xuyên sử dụng từ những
thumb|right|Các thao tác bước xoay [[Rubik|khối lập phương Rubik tạo thành nhóm khối lập phương Rubik.]] Trong toán học, một **nhóm** (group) là một tập hợp các phần tử được trang bị một phép toán
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
Những Câu Hỏi Lớn đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
**Người tiếp xúc UFO** (tiếng Anh: _Contactees_) là những người tuyên bố đã từng tiếp xúc với người ngoài hành tinh. Một số chủ thể kể lại có những cuộc gặp gỡ đang diễn ra,
**Thomas Andrew "Tom" Lehrer** (9 tháng 4 năm 1928 - 26 tháng 7 năm 2025) là một nhạc sĩ-ca sĩ, nghệ sĩ piano, nhà trào phúng và nhà toán học, nửa sau sự nghiệp chuyển
nhỏ|Biểu tượng **vô tận** **Vô hạn, vô cực, vô tận** (ký hiệu: ∞) là một khái niệm mô tả một cái gì đó mà không có bất kỳ giới hạn nào, hoặc một cái gì
Trong lý thuyết số, số nguyên tố được gọi là **số nguyên tố Sophie Germain** nếu cũng là số nguyên tố. Số của số nguyên tố
thumb| với giá trị . Trong số học, **lập phương** của một số _n_ có nghĩa là nhân 3 lần giá trị của nó với nhau: :. Hay cũng có thể hiểu là lấy tích
**Hằng số Gelfond–Schneider** hay **số Hilbert** là hai mũ căn bậc hai của hai: :2 = ... và được chứng minh là số siêu việt bởi Rodion Kuzmin năm 1930. Năm 1934, Aleksandr Gelfond và
Bộ 2 cuốn sách tìm hiểu về lịch sử toán học: Toán Học Một Thiên Tiểu Thuyết - Những Câu Hỏi Lớn Toán Học - Toán Học Một Thiên Tiểu Thuyết Hầu hết mọi người
Những Câu Hỏi Lớn - Toán Học NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại
NHỮNG CÂU HỎI LỚN đề cập đến những vấn đề cơ bản trong khoa học tự nhiên và xã hội, nhưng vẫn khiến những bộ óc vĩ đại trong lịch sử đau đầu. Từ những
thumb|[[Đồ thị nửa lôgarit của các nghiệm của phương trình cho số nguyên , , và , với . Dải màu xanh lá cây đánh dấu các giá trị được chứng
Lý thuyết số sơ cấp - Phương pháp sơ cấp trong lý thuyết số - Bản ĐB (Bìa cứng - Chữ kí của tác giả: GS.Ngô Bảo Châu) - Tác giả: GS. Ngô Bảo
Lý thuyết số sơ cấp - Phương pháp sơ cấp trong lý thuyết số - Tác giả: GS. Ngô Bảo Châu - TS. Đỗ Việt Cường - Nhà xuất bản Đại học Quốc gia Hà
Lý thuyết số, từ nhiều góc độ, được xem là điểm khởi đầu của toán học. Không chỉ là nơi khơi nguồn cho nhiều nhánh toán học phát triển, mà nó còn đem đến những
thế=Groups of two to twelve dots, showing that the composite numbers of dots (4, 6, 8, 9, 10, and 12) can be arranged into rectangles but the prime numbers cannot|nhỏ| Hợp số có thể được
**Leonhard Euler** ( , ; 15 tháng 4 năm 170718 tháng 9 năm 1783) là một nhà toán học, nhà vật lý học, nhà thiên văn học, nhà lý luận và kỹ sư người Thụy
**Johann Carl Friedrich Gauß** (; ; ; 30 tháng 4 năm 1777 – 23 tháng 2 năm 1855) là một nhà toán học và nhà khoa học người Đức tài năng, người đã có nhiều
**Blaise Pascal** (; 19 tháng 6 năm 1623 – 19 tháng 8 năm 1662) là nhà toán học, vật lý, nhà phát minh, tác gia, và triết gia Công giáo người Pháp. Là cậu bé
 Siêu Nhí Khám Phá: Toán Tư Duy - Phát Triển Toàn Diện IQ Toán Học Dành Cho Bé Từ 3 - 4 Tuổi - 1980Edu
Siêu Nhí Khám Phá: Toán Tư Duy - Phát Triển Toàn Diện IQ Toán Học Dành Cho Bé Từ 3 - 4 Tuổi - 1980Edu  Sách - Phiếu Bài Tập Cuối Tuấn Môn Toán Lớp 3 - Biên Soạn Theo Chương Trình GDPT Mới - Hồng Ân
Sách - Phiếu Bài Tập Cuối Tuấn Môn Toán Lớp 3 - Biên Soạn Theo Chương Trình GDPT Mới - Hồng Ân  Sách Vòng lặp OODA (Phương pháp ra quyết định và hành động tối ưu trong công việc)
Sách Vòng lặp OODA (Phương pháp ra quyết định và hành động tối ưu trong công việc)  Combo Sách Học Tiếng Nhật Hay( Bản Tiếng Nhật): Tiếng Nhật Cho Mọi Người - Trình Độ Sơ Cấp 1 - Bản Tiếng Nhật - (Tái Bản) + Tiếng Nhật Cho Mọi Người - Sơ Cấp 2 - Bản Tiếng Nhật (Bản Mới) ( Tặng Kèm Bookmark Green Life )
Combo Sách Học Tiếng Nhật Hay( Bản Tiếng Nhật): Tiếng Nhật Cho Mọi Người - Trình Độ Sơ Cấp 1 - Bản Tiếng Nhật - (Tái Bản) + Tiếng Nhật Cho Mọi Người - Sơ Cấp 2 - Bản Tiếng Nhật (Bản Mới) ( Tặng Kèm Bookmark Green Life )  Bách Khoa Tri Thức Phổ Thông - 10 Vạn Câu Hỏi Vì Sao? (Bìa Cứng)
Bách Khoa Tri Thức Phổ Thông - 10 Vạn Câu Hỏi Vì Sao? (Bìa Cứng)  Combo Sói già Phố Wall trọn bộ 2 tập tái bản (tặng kèm bookmark thiết kế aha)
Combo Sói già Phố Wall trọn bộ 2 tập tái bản (tặng kèm bookmark thiết kế aha)  Vui học cùng Sư tử - Sư tử học toán
Vui học cùng Sư tử - Sư tử học toán  Sách - Phân Loại Và Giải Nhanh Bài Tập Hóa Hữu Cơ - Hồng Ân
Sách - Phân Loại Và Giải Nhanh Bài Tập Hóa Hữu Cơ - Hồng Ân  Sách - Đề Kiểm Tra Toán Lớp 6 - Combo 2 Tập - Biên Soạn Theo Chương Trình GDPT Mới - Hồng Ân
Sách - Đề Kiểm Tra Toán Lớp 6 - Combo 2 Tập - Biên Soạn Theo Chương Trình GDPT Mới - Hồng Ân  Sách - Học Tiếng Anh Bằng Hình Ảnh Lớp 1 - Hồng Ân
Sách - Học Tiếng Anh Bằng Hình Ảnh Lớp 1 - Hồng Ân  Combo The Small Big – Tuyệt Chiêu Thuyết Phục, Hạ Gục Khách Hàng + 7 Loại Hình Thông Minh (Bộ 2 Cuốn)
Combo The Small Big – Tuyệt Chiêu Thuyết Phục, Hạ Gục Khách Hàng + 7 Loại Hình Thông Minh (Bộ 2 Cuốn)  Một Thế Giới Không Có Đàn Bà (Trinh Thám Việt Nam)
Một Thế Giới Không Có Đàn Bà (Trinh Thám Việt Nam)  Combo Trọn Bộ 5 Cuốn Chiến Tranh Tiền Tệ ( Tập 1+2+3+4+5 )
Combo Trọn Bộ 5 Cuốn Chiến Tranh Tiền Tệ ( Tập 1+2+3+4+5 )  (Bìa cứng có áo) EVIE VÀ CHUYẾN PHIÊU LƯU Ở RỪNG NHIỆT ĐỚI - Matt Haig - Thaihabooks
(Bìa cứng có áo) EVIE VÀ CHUYẾN PHIÊU LƯU Ở RỪNG NHIỆT ĐỚI - Matt Haig - Thaihabooks  Sách - Tập viết lớp 1 tập 1 + 2 (KV)
Sách - Tập viết lớp 1 tập 1 + 2 (KV)  Nghệ Thuật Quản Lý Tài Chính Cá Nhân
Nghệ Thuật Quản Lý Tài Chính Cá Nhân  Tại Sao Các Quốc Gia Thất Bại (Tái bản năm 2024) (Nobel Kinh tế 2024)
Tại Sao Các Quốc Gia Thất Bại (Tái bản năm 2024) (Nobel Kinh tế 2024)  Combo 3 Quyển Ehon Nhật Bản - Ehon Kỹ Năng Sống Cho Bé Trai
Combo 3 Quyển Ehon Nhật Bản - Ehon Kỹ Năng Sống Cho Bé Trai  Chinh Phục Đề Thi 9 Vào 10 Chuyên Hóa Học
Chinh Phục Đề Thi 9 Vào 10 Chuyên Hóa Học  Combo Nghệ Thuật Xây Dựng Công Ty Thành Công: Vĩ Đại Do Lựa Chọn, Từ Tốt Đến Vĩ Đại, Xây Dựng Để Trường Tồn
Combo Nghệ Thuật Xây Dựng Công Ty Thành Công: Vĩ Đại Do Lựa Chọn, Từ Tốt Đến Vĩ Đại, Xây Dựng Để Trường Tồn  Combo Truyện Trinh Thám hấp dẫn: Nguồn Cội - Origin + Biểu Tượng Thất Truyền / Sách Hay Của Dan Brown
Combo Truyện Trinh Thám hấp dẫn: Nguồn Cội - Origin + Biểu Tượng Thất Truyền / Sách Hay Của Dan Brown  Thơ gia đình yêu thương : Thơ về ông,bà,bố,mẹ - lẻ tùy chọn ( Đại Mai )
Thơ gia đình yêu thương : Thơ về ông,bà,bố,mẹ - lẻ tùy chọn ( Đại Mai )  Sách Cảnh Sắc Đà Lạt - Xứ Ngàn Hoa: Tranh Và Ký Họa
Sách Cảnh Sắc Đà Lạt - Xứ Ngàn Hoa: Tranh Và Ký Họa  Tiếng Việt Cơ Sở Dành Cho Người Nước Ngoài Quyển 1
Tiếng Việt Cơ Sở Dành Cho Người Nước Ngoài Quyển 1  CẨM NANG MUA BÁN NHÀ
CẨM NANG MUA BÁN NHÀ  Combo Big 4 Bộ Đề Tự Kiểm Tra 4 Kỹ Năng Nghe - Nói - Đọc - Viết (Cơ Bản Và Nâng Cao) Tiếng Anh Lớp 9 (2 Tập)
Combo Big 4 Bộ Đề Tự Kiểm Tra 4 Kỹ Năng Nghe - Nói - Đọc - Viết (Cơ Bản Và Nâng Cao) Tiếng Anh Lớp 9 (2 Tập)  Sách - Hiền Ngu Nhân Duyên Kinh Luận Giải - Tổ In Ấn Kinh Phật
Sách - Hiền Ngu Nhân Duyên Kinh Luận Giải - Tổ In Ấn Kinh Phật  Understanding Digital Marketing - Thông Thạo Digital Marketing
Understanding Digital Marketing - Thông Thạo Digital Marketing  OSHO - Trò Chuyện Với Vĩ Nhân
OSHO - Trò Chuyện Với Vĩ Nhân  Trạm Đọc | Kỹ Năng Sinh Tồn Cho Trẻ: Trong nhà chưa chắc đã an toàn đâu nhé!
Trạm Đọc | Kỹ Năng Sinh Tồn Cho Trẻ: Trong nhà chưa chắc đã an toàn đâu nhé!  Combo OCEAN – Thuyết Minh Trực Quan Nhất Về Đại Dương và Những Câu Hỏi Lớn - Vũ Trụ
Combo OCEAN – Thuyết Minh Trực Quan Nhất Về Đại Dương và Những Câu Hỏi Lớn - Vũ Trụ  Combo Giảm giá sâu 3 cuốn sách: Quản trị mục tiêu bằng KPI, BSC & OKR, Sách 100 + 25 Câu hỏi BSC & KPI và Sách Hiện tượng RĐ - Sống sót trong dòng xoáy chuyển đổi
Combo Giảm giá sâu 3 cuốn sách: Quản trị mục tiêu bằng KPI, BSC & OKR, Sách 100 + 25 Câu hỏi BSC & KPI và Sách Hiện tượng RĐ - Sống sót trong dòng xoáy chuyển đổi  Cách Những Công Ty Lớn Nhất Thế Giới Sinh Tồn
Cách Những Công Ty Lớn Nhất Thế Giới Sinh Tồn  Truyện cổ tích Kazakhstan - Tập 2
Truyện cổ tích Kazakhstan - Tập 2  Sách - Giúp Trí Nhớ Chuỗi Phản Ứng Hóa Học - Hồng Ân
Sách - Giúp Trí Nhớ Chuỗi Phản Ứng Hóa Học - Hồng Ân  Sách - Combo Phiếu Bài Tập Cuối Tuấn Môn Toán + Tiếng Việt + Tiếng Anh Lớp 4 - Biên Soạn Theo Chương Trình GDPT Mới
Sách - Combo Phiếu Bài Tập Cuối Tuấn Môn Toán + Tiếng Việt + Tiếng Anh Lớp 4 - Biên Soạn Theo Chương Trình GDPT Mới  Combo 2 cuốn sách khởi nghiệp hay: Bước Đi Ngẫu Nhiên Trên Phố Wall + Phương pháp đầu tư Warren Buffett (tặng kèm bookmark thiết kế aha)
Combo 2 cuốn sách khởi nghiệp hay: Bước Đi Ngẫu Nhiên Trên Phố Wall + Phương pháp đầu tư Warren Buffett (tặng kèm bookmark thiết kế aha)  Tập Viết Chữ Hoa
Tập Viết Chữ Hoa  10 Thói Quen Của Triệu Phú Tự Thân
10 Thói Quen Của Triệu Phú Tự Thân  Trò Chơi Màu Sắc Dành Cho Gấu Mèo Chester Và Kẻ Bắt Nạt To Xác Xấu Xa – A Color Game For Chester Raccon
Trò Chơi Màu Sắc Dành Cho Gấu Mèo Chester Và Kẻ Bắt Nạt To Xác Xấu Xa – A Color Game For Chester Raccon  Tĩnh Lặng ( Tái Bản 2021 )
Tĩnh Lặng ( Tái Bản 2021 )  Sách Ehon - Chơi Thể Thao Cùng Kenta (Combo 6 cuốn)
Sách Ehon - Chơi Thể Thao Cùng Kenta (Combo 6 cuốn)  Giáo Trình Marugoto - Sơ Cấp 2 - A2 - Hiểu Biết Ngôn Ngữ Văn Hóa Nhật _FN
Giáo Trình Marugoto - Sơ Cấp 2 - A2 - Hiểu Biết Ngôn Ngữ Văn Hóa Nhật _FN  Toán Học Cho Trẻ Mẫu Giáo: Lớp Lá 2
Toán Học Cho Trẻ Mẫu Giáo: Lớp Lá 2  Sách - Kinh Vạn Phật - Bìa Da - Tổ In Ấn Kinh Phật
Sách - Kinh Vạn Phật - Bìa Da - Tổ In Ấn Kinh Phật  Sách Dạy Con Làm Giàu (Tập 1) Để Không Có Tiền Vẫn Tạo Ra Tiền
Sách Dạy Con Làm Giàu (Tập 1) Để Không Có Tiền Vẫn Tạo Ra Tiền  100 Truyện Cổ Tích Thế Giới + 100 Truyện Cổ Tích Việt Nam (Bìa Cứng)
100 Truyện Cổ Tích Thế Giới + 100 Truyện Cổ Tích Việt Nam (Bìa Cứng)  Sách - Succeed in KET - 10 Practice Tests (Kèm 01 Đĩa MP3) - Nhân Trí Việt
Sách - Succeed in KET - 10 Practice Tests (Kèm 01 Đĩa MP3) - Nhân Trí Việt  Chuyện Phiêu Lưu Của Mít Đặc Và Các Bạn (Tái Bản 2018)
Chuyện Phiêu Lưu Của Mít Đặc Và Các Bạn (Tái Bản 2018)  Bộ Não Tí Hon Tập 1: Cái Nôi Của Thiên Tài _FN
Bộ Não Tí Hon Tập 1: Cái Nôi Của Thiên Tài _FN  Tổng Quan Về Tarot (Bìa Cứng)
Tổng Quan Về Tarot (Bìa Cứng)  Tự Giác Gọn Gàng - Xây Dựng Thói Quen Dọn Dẹp Cho Trẻ Từ 3 Tuổi
Tự Giác Gọn Gàng - Xây Dựng Thói Quen Dọn Dẹp Cho Trẻ Từ 3 Tuổi  270 Đề Và Bài Văn Hay 12
270 Đề Và Bài Văn Hay 12  Trật Tự Thế Giới (Tái Bản)
Trật Tự Thế Giới (Tái Bản)  Mèo Chiến Binh - Bí Mật Rừng Sâu
Mèo Chiến Binh - Bí Mật Rừng Sâu  KTHD. Horrible Geography - Sông Ngòi Xông Xênh (Tái Bản)
KTHD. Horrible Geography - Sông Ngòi Xông Xênh (Tái Bản)  Search Inside Yourself - Tạo Ra Lợi Nhuận Vượt Qua Đại Dương Và Thay Đổi Thế Giới
Search Inside Yourself - Tạo Ra Lợi Nhuận Vượt Qua Đại Dương Và Thay Đổi Thế Giới  Sách Khi Mọi Điểm Tựa Đều Mất (Tái Bản 2019)
Sách Khi Mọi Điểm Tựa Đều Mất (Tái Bản 2019)  Định Lý Cuối Cùng Của Fermat - Một Mật Mã Huyền Bí Và Định Mệnh
Định Lý Cuối Cùng Của Fermat - Một Mật Mã Huyền Bí Và Định Mệnh  Định Lý Cuối Cùng Của Fermat
Định Lý Cuối Cùng Của Fermat  Khoa Học Khám Phá - Định Lý Cuối Cùng Của Fermat
Khoa Học Khám Phá - Định Lý Cuối Cùng Của Fermat  Khoa Học Khám Phá - Định Lý Cuối Cùng Của Fermat - Hành Trình Đi Tìm Lời Giải Cho Bài Toán Khó Bậc Nhất Trong Lịch Sử (Tái Bản 2023)
Khoa Học Khám Phá - Định Lý Cuối Cùng Của Fermat - Hành Trình Đi Tìm Lời Giải Cho Bài Toán Khó Bậc Nhất Trong Lịch Sử (Tái Bản 2023)  (In lần thứ 8 năm 2023 – Tủ sách Khoa học khám phá) - ĐỊNH LÝ CUỐI CÙNG CỦA FERMAT - Simon Singh – Phạm Văn Thiều, Phạm Việt Hưng dịch - Nhà xuất bản Trẻ
(In lần thứ 8 năm 2023 – Tủ sách Khoa học khám phá) - ĐỊNH LÝ CUỐI CÙNG CỦA FERMAT - Simon Singh – Phạm Văn Thiều, Phạm Việt Hưng dịch - Nhà xuất bản Trẻ  ĐỊNH LÝ CUỐI CÙNG CỦA FERMAT
ĐỊNH LÝ CUỐI CÙNG CỦA FERMAT  ĐỊNH LÝ CUỐI CÙNG CỦA FERMAT - Simon Singh - Phạm Văn Thiều, Phạm Việt Hưng dịch - (bìa mềm)
ĐỊNH LÝ CUỐI CÙNG CỦA FERMAT - Simon Singh - Phạm Văn Thiều, Phạm Việt Hưng dịch - (bìa mềm)  Sách - Định Lý Cuối Cùng Của Fermat - NXB Trẻ
Sách - Định Lý Cuối Cùng Của Fermat - NXB Trẻ  Combo Sách Kiến Thức Bách Khoa Hay : Những Câu Hỏi Lớn Vật Lý + Những Câu Hỏi Lớn Toán Học ( Tặng Kèm Postcard HAPPY LIFE )
Combo Sách Kiến Thức Bách Khoa Hay : Những Câu Hỏi Lớn Vật Lý + Những Câu Hỏi Lớn Toán Học ( Tặng Kèm Postcard HAPPY LIFE )  Những Câu Hỏi Lớn - Toán Học
Những Câu Hỏi Lớn - Toán Học  Những Câu Hỏi Lớn Toán Học ( Tái bản)
Những Câu Hỏi Lớn Toán Học ( Tái bản)  Những Câu Hỏi Lớn Toán Học
Những Câu Hỏi Lớn Toán Học  Những Câu Hỏi Lớn Toán Học (Tái Bản)
Những Câu Hỏi Lớn Toán Học (Tái Bản)  Bộ 2 cuốn sách tìm hiểu về lịch sử toán học: Toán Học Một Thiên Tiểu Thuyết - Những Câu Hỏi Lớn Toán Học
Bộ 2 cuốn sách tìm hiểu về lịch sử toán học: Toán Học Một Thiên Tiểu Thuyết - Những Câu Hỏi Lớn Toán Học  Sách - Những câu hỏi lớn – Toán học
Sách - Những câu hỏi lớn – Toán học  Lý thuyết số sơ cấp - Phương pháp sơ cấp trong lý thuyết số - Bản ĐB (Bìa cứng - Chữ kí của tác giả: GS.Ngô Bảo Châu)
Lý thuyết số sơ cấp - Phương pháp sơ cấp trong lý thuyết số - Bản ĐB (Bìa cứng - Chữ kí của tác giả: GS.Ngô Bảo Châu)  Lý thuyết số sơ cấp - Phương pháp sơ cấp trong lý thuyết số
Lý thuyết số sơ cấp - Phương pháp sơ cấp trong lý thuyết số  LÝ THUYẾT SỐ SƠ CẤP - Phương Pháp Sơ Cấp Trong Lý Thuyết Số - Ngô Bảo Châu, Đỗ Việt Cường - NXB Đại Học Quốc Gia Hà Nội
LÝ THUYẾT SỐ SƠ CẤP - Phương Pháp Sơ Cấp Trong Lý Thuyết Số - Ngô Bảo Châu, Đỗ Việt Cường - NXB Đại Học Quốc Gia Hà Nội  Nỗi Bất An Trong Văn Hoá - Sigmund Freud
Nỗi Bất An Trong Văn Hoá - Sigmund Freud  Sách - Chư Kinh Nhật Tụng - Các bộ kinh Phật quan trọng cho Phật tử tụng niệm mỗi ngày
Sách - Chư Kinh Nhật Tụng - Các bộ kinh Phật quan trọng cho Phật tử tụng niệm mỗi ngày  Sách tiếng Anh - Lily Quench And The Hand of Manuelo
Sách tiếng Anh - Lily Quench And The Hand of Manuelo  Wolfoo Ehon - Người Bạn Thân Nhất Của Tớ
Wolfoo Ehon - Người Bạn Thân Nhất Của Tớ  Sách - Trà kinh (Bìa cứng) - Nhã Nam Official
Sách - Trà kinh (Bìa cứng) - Nhã Nam Official  Thư Viết Từ Hà Nội - Bom Đã Rơi Trên Hè Phố Thủ Đô
Thư Viết Từ Hà Nội - Bom Đã Rơi Trên Hè Phố Thủ Đô  Thảm lót sàn xe ô tô BMW 1 series 2020- nhãn hiệu Macsim 3W - chất liệu nhựa TPE đúc khuôn cao cấp - màu đen
Thảm lót sàn xe ô tô BMW 1 series 2020- nhãn hiệu Macsim 3W - chất liệu nhựa TPE đúc khuôn cao cấp - màu đen  NGOẠI NGỮ KHÓ ĐẤY NHƯNG BẠN TỰ HỌC ĐƯỢC - Bí quyết tự học chinh phục song ngữ Anh, Trung - Việt Lê - (bìa mềm)
NGOẠI NGỮ KHÓ ĐẤY NHƯNG BẠN TỰ HỌC ĐƯỢC - Bí quyết tự học chinh phục song ngữ Anh, Trung - Việt Lê - (bìa mềm)  Tự Chữa Lành - Làm Sao Để Khai Sáng - Tập 2
Tự Chữa Lành - Làm Sao Để Khai Sáng - Tập 2  Tủ sắt quần áo dày sơn tĩnh điện 3 cửa 1m2 - 1m8 – TSDT09
Tủ sắt quần áo dày sơn tĩnh điện 3 cửa 1m2 - 1m8 – TSDT09  Nghiến răng nỗ lực, vươn lên dẫn đầu
Nghiến răng nỗ lực, vươn lên dẫn đầu  Mẹ Biết Đủ, Con Tự Chủ
Mẹ Biết Đủ, Con Tự Chủ  ジョジョリオン 22 (ジャンプコミックス) - JOJORION 22
ジョジョリオン 22 (ジャンプコミックス) - JOJORION 22  Hồi Đáp Từ 40 Năm Học Yêu ( Tặng Kèm Bookmark )
Hồi Đáp Từ 40 Năm Học Yêu ( Tặng Kèm Bookmark )  Sách - Ngữ văn lớp 12 - Ngữ liệu đọc hiểu mở rộng
Sách - Ngữ văn lớp 12 - Ngữ liệu đọc hiểu mở rộng  Những Nhà Tư Tưởng Lớn - Hegel Trong 60 Phút
Những Nhà Tư Tưởng Lớn - Hegel Trong 60 Phút  Sách - Chuyên Đề Bồi Dưỡng Học Sinh Giỏi Toán THCS Bất Đẳng Thức Và Cực Trị Trong Đại Số + Hình Học Phẳng - Khang Việt Book
Sách - Chuyên Đề Bồi Dưỡng Học Sinh Giỏi Toán THCS Bất Đẳng Thức Và Cực Trị Trong Đại Số + Hình Học Phẳng - Khang Việt Book 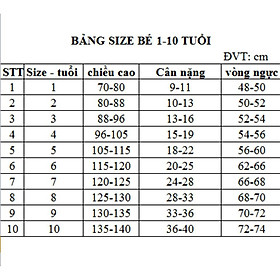 Rập đàm cổ trò bé gái giấy A0 mã R439 (BẢN VẼ)
Rập đàm cổ trò bé gái giấy A0 mã R439 (BẢN VẼ)  Rèm Che Nắng Xe Toyota Wigo Hàng Loại 1 MR Ô TÔ
Rèm Che Nắng Xe Toyota Wigo Hàng Loại 1 MR Ô TÔ  Nghe Nói Tôi Rất Nghèo - Tập 3
Nghe Nói Tôi Rất Nghèo - Tập 3  Chứng minh của Wiles về Định lý cuối cùng của Fermat
Chứng minh của Wiles về Định lý cuối cùng của Fermat